Geometrical Modelling of Plain Weft Knitted Fabrics
Knitted Fabrics - loop formation and calculations
In order to produce the fabric with maximum cover factor with the minimum weight, it’s only possible when GH is the distance between the loops in a horizontal direction and KJ is the correct length between the loops in a longitudinal direction. In this article Dr Vojislav explains geometrical pattern of knitted fabrics.
The model of the relationship between the loop, the order of the loop length and the length of the loop in the loop was developed. The coordinate values of the points illustrated were calculated which define the central axis of yarn using the spline curves in Abaqus / CAE. Abaqus / CAE calculates the shape of the curve using a cubic spline fit between all points along the spline; In addition, the first and second derivatives of the spline are continuous. The 3D models of plain weft knit fabrics can be generated by sweeping the circular cross section of the yarn along the central axis of the yarn. Yarns were assumed to be incompressible in nature.
Knitted fabrics have a good stretch property that offers better conformability and avoids excessive pressure between the garment and body. Many researchers have analyzed the geometrical pattern of knitted fabrics. In 1926 Chamberlain presented a two-dimensional loop structure of the plain knitted fabric. He proposed that the theoretically correct fabric, in which GH represents the distance between the centres of two loops, GKH represent the equilateral triangle and KJ bisect the equilateral triangle.
In Chamberlain’s model, there is no consideration of loop in the third dimension in order to produce the fabric with a maximum cover factor, but it is only possible when GH is the distance between the loops in a horizontal direction and KJ is the correct length between the loops in the longitudinal direction. So the length of the loop cannot be predicted with high accuracy. In 1947 Peirce developed a geometric model of plain weft knit fabric on the assumption that the loop formed from the circular arc and straight line and the yarn central axis follows a path on the surface of cylinder following the direction of a course. In order to develop the relationship of stitch length in terms of yarn diameter, wales and course spacing.
Geometry and structure of loops
Knitted fabrics have a good stretch property which offers better conformability and avoids excessive pressure between the garment and body [1]. Many researchers analysed the geometrical model of knitted fabrics. In 1926 Chamberlain [2] presented a two-dimensional loop structure of the plain knitted fabric. He proposed that the theoretically correct fabric as shown in Equation-1, in which GH represents the distance between the centres of two loops, GKH represent the equilateral triangle and KJ bisect the equilateral triangle. In order to produce the fabric with maximum cover factor with the minimum weight, it’s only possible when GH is the distance between the loops in a horizontal direction and KJ is the correct length between the loops in a longitudinal direction.
-
![loop-minimum-area-of-intersection-formula]()
Equation-1: The minimum area of intersection obtained when; -
![The relationship between course and wale in the fabric is expressed]()
Equation-2: The relationship between course and wale in the fabric is expressed ![Diameter and stitch length of the yarn can be calculated by the following equations [2]]()
Equation-3: Diameter and stitch length of the yarn can be calculated by the following equations [2] -
![Stitch length of yarn]()
Equation-4: Stitch length of yarn -
![Stitch length of yarn]()
Equation-5: stitch length of yarn -
![Stitch length of yarn]()
Equation-6: Stitch length of yarn -
![Stitch length of yarn]()
Equation-7: Stitch length of yarn. where w is the wale spacing -
![Chamberlain’s jammed plain knitted loop]()
Figure-1: Chamberlain’s jammed plain knitted loop
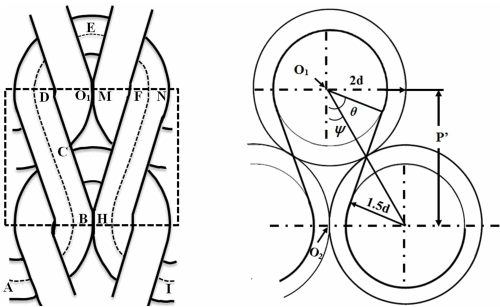
In Chamberlain’s model, there was no consideration of a loop in the third dimension so the length of the loop cannot be predicted with high accuracy. In 1947 Peirce [3] developed a geometrical model of plain weft knitted fabric on the assumption that the loop composed of a circular arc and straight line and the yarn central axis follows a path on the surface of cylinder following the direction of a course. In order to develop the relationship of stitch length in terms of yarn diameter, wales and course spacing he considered the flat structure of plain weft knitted fabric as shown in Figure 2. In his compact planned structure, the course ( p’ ) and wales ( w ) spacing can be calculated by Equation 8 & 9 respectively,
-
![Course Spacing]()
Equation-8: Course Spacing -
![Wales Spacing]()
Equation-9: Wales Spacing -
![Stitch length of loop equation]()
Equation-10: Stitch length of loop can be calculated with this equation -
![]()
Figure 2: Planed structure of Peirce’s loop - y and q as shown in Figure-2 can be calculated by the following expressions:
![]()
![]()
-
![]()
Hence stitch length becomes:l/4 =2.8428d+1.3229d=4.1657r, stitch length (l)= 16.6628d
In all the above equations there was no consideration of the bending effect of yarn. In order to include this effect, he assumed that these loops laid on the cylinder which gives three-dimensional effects to the knitted loop. He found that the radius of curvature R was only satisfied in order to provide space for interlocking when it equals 4.172 times the diameter of yarn as shown in Figure 3.
The wales spacing is not affected in three-dimensional loop structure but course spacing as it was observed by him in a plane of the cloth is:
-
![Equation-11]()
Equation-11: -
![3D dimensional Peirce’s loop structure of plain weft knitted fabric]()
Figure-3: 3D dimensional Peirce’s loop structure of plain weft knitted fabric
He also developed a relationship of wales spacing, course spacing and stitch length for open structure plain weft knitted fabric as shown in Equation 12, 13, and 14 respectively. Peirce suggested that more open structures than the one he considers could be examined by inserting a suggested a straight yarn with the length of ed in the crown of the loop, and a length structure by inserting a space ed along the wale line O1O2 and by inserting a straight line parallel to the course line. Similarly, a straight length xd was inserted in the centre of each loop. The increase in course spacing was virtually equal to the added length of yarn.
-
![]()
Equation-12: -
![]()
Equation-13: -
![]()
Equation-14:
Shinn [4] also analysed the two dimensional geometrical model of plain weft knitted fabric based on Peirce’s model [3]. He compared the experimental results with the theoretical results obtained from expression generated from the Peirce two dimensional geometrical models. He also modified the Tompkins’s formula [4] by which weight per square yard was predicted by using relations of stitch length, courses and wales spacing developed by Peirce.
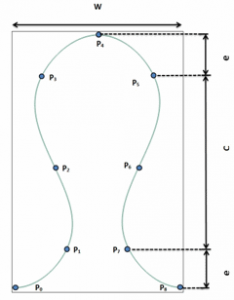
In 1955 Leaf and Glaskin [5] pointed out that the stable knitted fabric loop structure could not be produced by the model proposed by the Peirce [3]. They showed that the Peirce considered the radius of curvature R = 4.172d for all types of the loop which gave the discontinuity in the torsion of yarn and eventually affected the shape of loops. They proposed a geometrical model of plain weft knitted fabric in which the central axis of yarn passes over a series of a circular cylinder and their model composed of circular arcs as shown in Figure 4.
-
![Leaf and Glaskin’s model of plain weft knitted fabric]()
Figure-4: Leaf and Glaskin’s model of plain weft knitted fabric -
![]()
Equation-15: where d is the diameter of yarn, W and C are the courses and wales spacing respectively. -
![]()
Equation-16: where d is the diameter of yarn, W and C are the courses and wales spacing respectively. -
![]()
Equation-17: where d is the diameter of yarn, W and C are the courses and wales spacing respectively. - In 1959 Munden [6-126] developed the relationships between stitch length and wale and course spacing. He proved that the ratios between course and wale spacing per stitch length were independent of fabric cover factor. The developed relationships are as follows:
-
![]()
Equation-18: -
![]()
Equation-19: -
![]()
Equation-20: -
![]()
Equation-21: -
![]()
Equation-22: Where K1, K2, K3 and K4 are constant values which can be determined experimentally on the basis of actual configuration (wet or dry relax state) of a knitted loop.
Hurd and Doyle [8], Postle [9] and Kurbak [10] also studied the geometry of plain weft knitted fabrics. Furthermore, Demiroz and Dias [11] developed a mathematical model to generate 3D images of plain weft knitted fabric. They developed a stitched model by using cubic-spline as the central axis. The software relating to their developed model required input parameters such as yarn diameter, stitch length, course and wales spacing and other fabric parameters were calculated by a software program developed using C programing language.
Choi and Lo [12] developed a model of plain weft knitted fabric to describe the mechanical properties and dimensional change in a fabric through energy approach. Their model is also capable of predicting the biaxial tensile property of knitted fabrics.
Kyosev et al. [13] developed two models of plain weft knitted fabrics. Their first model is a pure geometrical model based on research work done by Choi and Lo [12] taking into consideration the yarn cross-section as elliptical. Their second model was made in considering discretization of yarn into a small element and mechanical interaction between the yarns.
Ying-lin, L., et al., [14] developed geometrical models of weft knitted fancy structures on the basis of Non-uniform Rational B-splines (NURBS) curve. They generated the yarn central axis by using a set of points at an intermeshing position of yarn adopting NURBS method and created the solid shape of a knit loop by sweeping the sphere along the yarn. They developed a program to generate a 3D surface loop model by using Visual C++ programing language and Open GL.
Plain weft knitted fabrics were used in this study. Plain weft knitted structure is normally used for single jersey fabrics for sportswear. Different types of yarns were used to develop weft knitted fabrics to evaluate the effectiveness of the developed method.
The fabric specifications are shown in Table 1 and their surface macrostructures are illustrated in Figure 5.
| Fabric Code | Fibre Type | Yarn Count (Tex) | wpc | cpc | SL(mm) | t (mm) | Areal Density(g/m2) |
|---|---|---|---|---|---|---|---|
| F1 | Polyester (MF) | 27.0 | 3.2 | 5.6 | 8.220 | 0.49 | 40.4 |
| F2 | Polyester (MF) | 20.0 | 6.4 | 9.6 | 4.930 | 0.47 | 61.0 |
| F3 | Polyester (MF) | 27.0 | 7.4 | 9.0 | 5.020 | 0.49 | 92.0 |
| F4 | Cotton (SF) | 40.0 | 6.0 | 7.5 | 5.910 | 0.8 | 104.62 |
| F5 | Viscose (MFF) | 33.5 | 6.0 | 9.6 | 5.083 | 0.648 | 102.3 |
MF: Monofilament; MFF: Multifilament; SF: Staple fibre; SL: Stitch length wpc: Wales per cm; cpc: Course per cm; and t: thickness
Finite Element Model
The parametric model of plain weft knitted fabric created by using the central axis of yarn is defined by the path shown in Figure 6 (a); but the actual parameters of the fabric such as, courses and wales per centimetre were used. Parameter ‘e’ can be determined by the average loop height (H) through image analysis using the following equation:
-
![]()
Equation-23:
The coordinate values of the points illustrated in Figure (a) were calculated which define the central axis of yarn using spline curve in Abaqus/CAE. Abaqus/CAE calculates the shape of the curve using a cubic spline fit between all points along the spline; in addition, the first and second derivatives of the spline are continuous. The 3D models of plain weft knitted fabrics can be generated by sweeping the circular cross- section of the yarn along the central axis of the yarn. Yarns were assumed to be incompressible in nature.
-
![Macrostructures of plain weft knitted fabrics-[F1]]()
Figure-5: Macrostructures of plain weft knitted fabrics [F1] ![Macrostructures of plain weft knitted fabrics-[F2]]()
Figure-5: Macrostructures of plain weft knitted fabrics [F2] ![Macrostructures of plain weft knitted fabrics-[F3]]()
Figure-5: Macrostructures of plain weft knitted fabrics [F3] ![Macrostructures of plain weft knitted fabrics-[F4]]()
Figure-5: Macrostructures of plain weft knitted fabrics [F4] ![Macrostructures of plain weft knitted fabrics-[F5]]()
Figure-5: Macrostructures of plain weft knitted fabrics [F5]
- A polyester plain weft knitted fabric (F3) model generated by the plug-in is shown in Figure 7.
![Geometrical parameter Yarn central axis]()
Figure 6: Geometrical parameter (a) Yarn central axis; -
![Geometrical parameter Thickness of fabric]()
Figure 6: Geometrical parameter – (b) Thickness of fabric -
![Geometrical model of fabric F3]()
Figure 7: Geometrical model of fabric F3
References
[1]. COOKE, B., The physical properties of weft knitted structures, in Advances in knitting technology, Au, K.F., Editor. 2011, Woodhead Publishing Ltd. p. 34-47.
[2]. Chamberlain, J., Hosiery yarns and fabrics : prepared for the textile trades advisory committee of the city of Leicester colleges of technology and art. 1926: Leicester : J. W. Hemmings & Capey.
[3]. Peirce, F.T., Geometrical principles applicable to the design of functional fabrics. Textile Research Journal, 1947. 17(3): p. 123-147.
[4]. Shinn, W.E., An engineering approach to jersey fabric construction. Textile Research Journal, 1955. 25(3): p. 270-277.
[5]. Tompkins, E., The science of knitting. 1914, New York: Wiley. 330 p.
[6]. Leaf, G.A.V. and Glaskin, A., The geometry of a plain knitted loop. Journal of the Textile Institute Transactions, 1955. 46(9): p. T587-T605.
[7]. Munden, D.L., The geometry and dimensional properties of plain-knit fabrics.
Journal of the Textile Institute Transactions, 1959. 50(7): p. T448-T471.
[8]. Hurd, J.C.H. and Doyle, P.J., Fundamental aspects of the design of knitted fabrics. Journal of the Textile Institute Proceedings, 1953. 44(8): p. 561-578.
[9]. Postle, R., Dimensional stability of plain-knitted fabrics. The Journal of The Textile Institute, 1968. 59(2): p. 65-77.
[10]. Kurbak, A., Plain knitted fabric dimensions (Part II). Textile Asia, 1998. 29(4): p. 36-44.
[11]. Demiroz, A. and Dias, T., A study of the graphical representation of plain- knitted structures part I: stitch model for the graphical representation of plain- knitted structures. The Journal of The Textile Institute, 2000. 91(4): p. 463-480.
[12]. Choi, K.F. and Lo, T.Y., An energy model of plain knitted fabric. Textile Research Journal, 2003. 73(8): p. 739-748.
[13]. Kyosev, Y., Angelova, Y., and Kovar, R., 3D modelling of plain weft knitted structures of compressible yarn. Research Journal of Textile and Apparel 2005. 9(1): p. 88.
[14]. Ying-lin, L., et al., 3D modelling and simulation of fancy fabrics in weft knitting Journal of Donghua University(English Edition), 2012. 29(4): p. 351-358




![Diameter and stitch length of the yarn can be calculated by the following equations [2]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Diameter-and-stitch-length-of-the-yarn-can-be-calculated-by-the-following-equations-2-300x46.png)
























![Macrostructures of plain weft knitted fabrics-[F1]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Macrostructures-of-plain-weft-knitted-fabrics-1-210x136.png)
![Macrostructures of plain weft knitted fabrics-[F2]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Macrostructures-of-plain-weft-knitted-fabrics-2-210x136.png)
![Macrostructures of plain weft knitted fabrics-[F3]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Macrostructures-of-plain-weft-knitted-fabrics-3-210x136.png)
![Macrostructures of plain weft knitted fabrics-[F4]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Macrostructures-of-plain-weft-knitted-fabrics-4-210x136.png)
![Macrostructures of plain weft knitted fabrics-[F5]](https://cdn.textileschool.com/wp-content/uploads/2018/10/Macrostructures-of-plain-weft-knitted-fabrics-5-210x136.png)